神经网络(neural network)的应用——自编码器(Autoencoder)
1. 自编码器简介
自编码器(Autoencoder,AE),是一种利用反向传播算法使得输出值等于输入值的神经网络,它先将输入压缩成潜在空间表征,然后通过这种表征来重构输出。
简单来说,就是可以自动实现编码与解码操作过程的网络模型,并且它的输入 x 与标签 y 相同,我们通过最小化标签 y 与输出 r 之间的误差,来优化自编码器模型。
因此,自编码器由两部分组成:
编码器:这部分能将输入压缩成潜在空间表征,可以用编码函数 h =f(x)表示。
解码器:这部分能重构来自潜在空间表征的输入,可以用解码函数 r =g(h)表示。
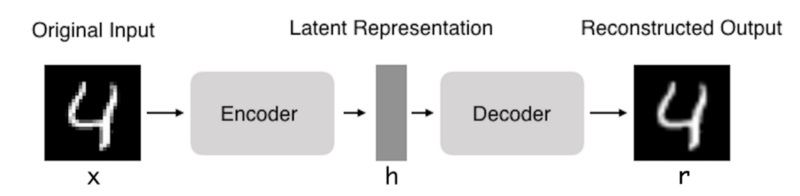
整个自编码器可以用函数g(f(x)) = r 来描述,其中输出r与原始输入 x 相近。
自编码器原理和各种变换的原理相似,都是将原始特征空间通过编码映射到一个新的编码空间,再由编码空间通过解码映射到解码空间。而当编码变换与解码变换符合某种条件时,解码空间和原始特征空间可以近似一致。
就像大名鼎鼎的傅里叶变换,通过它,可以把原始时域信号变换为频域信号,并且,频域信号可以通过反变换变换为时域信号。之所以要变换为频域信号,是为了获取原始信号在频域上的特征。同样的,对于自编码器的编码变换,也是为了获取不同角度,不同维度的特征(类似于SVM的核函数)。
按照Hinton的说法,自编码器的隐含层如果只有一层,其原理类似主成分分析(PCA),如果多个隐含层,每个隐含层都是受限玻尔兹曼机神经网。训练时,相当于先对每两层间进行无监督学习,将整个网络达到理想的初始化分布,最后再通过反向传播算法的有监督学习调整模型权重,这样可以解决网络过深带来的梯度弥散问题。
2. 自编码器的用途
数据可视化,数据降噪和降维被认为是自编码器的几个主要的实际应用。使用适当的维度和稀疏性约束,自编码器可以得到比PCA或其他类似技术更好的数据投影。
在自编码器中,中间的隐藏表达的维度往往维度比较低,因此可以被用作数据压缩,或者是特征降维。
不过自编码器原本不是专门用来做数据压缩的,它的作用就是可以作为很多神经网络的预训练,帮助提高模型的准确率。神经网络模型的训练需要大量具有标签的样本,而这样的数据通常是比较少的,更多的是无标签样本,而自编码器自监督的特性可以充分利用这些无标签样本,提前学习到有用的特征。接下来,把自编码器的编码器接入神经网络,进行训练。
2.1 降维与可视化
很明显,如果自编码器的只是单纯的将输入复制到输出中,那么它没有用处。所以实际上,我们希望通过训练自编码器将输入映射到 h 中,并且使表示函数 h 获得原始数据中有用的特征和属性,在这一过程中,输入到 h 的映射可以自动的帮助我们筛选特征,降低特征维度。
而想要让自编码器筛选有用特征,一种方法是约束 h 的维度小于 x ,在这种情况下,自编码器被称为欠完备(undercomplete)。通过训练不完整的表示,我们迫使自编码器学习训练数据的最有代表性(显著的)的特征。如果给自编码器的容量过大,则它可以复制 x 而不去提取关于数据分布的有用信息。
利用上述的方法,就达到了降维的作用。而当隐藏表达的维度降至三维或者二维时,就可以实现数据的可视化。
自编码器通过数据自动学习。这意味着在特定类型的输入中,自编码器可以表现出良好的结果,并且不需要任何新的结构,只需适当的训练数据即可。这种结构单一、无需标签的网络使用起来异常简单,并且常常会有不错的表现,所以使用地很广泛。
下面,看个例子,mnist数据集的二维可视化:
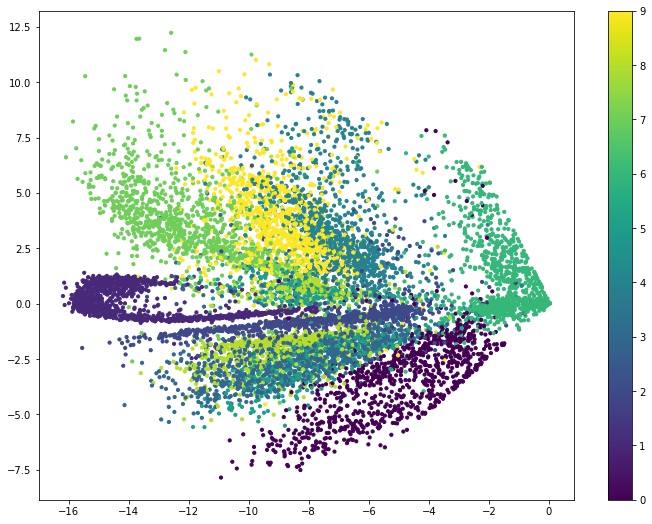
上图就是mnist数据集经过降维至二维后的可视化效果图。不同颜色的点代表不同的数字。
同样的,我们也可以降维到三维,形成空间可视化图:
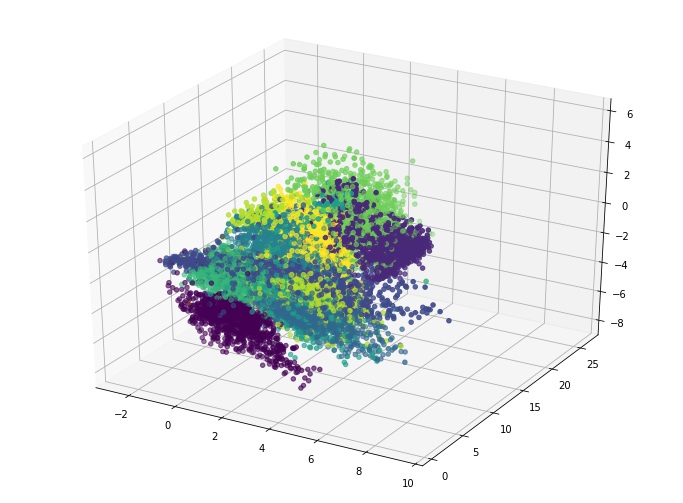
不过,它也不是没有缺点,首先,自编码器是数据相关的,是在给定的一组数据上进行训练的,因此它将得到与所用训练集数据相似的压缩结果,在这样的数据上表现优异,但就其通用性来说,效果并不好。比如在图像压缩领域,效果比不上JPEG这样的通用压缩技术。
3. 常见的自编码器与代码示例
3.1 简单自编码器和深度自编码器
from keras.layers import Input, Dense
from keras.models import Model
from keras.datasets import mnist
import numpy as np
encoding_dim=32
input_img = Input(shape=(784,))
encoded = Dense(encoding_dim, activation='relu')(input_img)
decoded = Dense(784, activation='sigmoid')(encoded)
autoencoder = Model(input_img, decoded)
encoder = Model(input_img, encoded)上面这种就是自编码器是最简单的形式,其中encoder是编码器,autoencoder是整个自编码器。
在这种形式中,基本上encoder的神经元个数都要少于输入的维度,因此Encoder在这里起到了降维的功能。
把encoding_dim=32换成encoding_dim=2或者encoding_dim=3就可以满足上图的可视化数据要求。
3.2 稀疏自编码器
除强加一个比输入更低维度的隐藏层外,还有其他一些方法可以限制自编码器的重构。包含正则化项的自编码器不需要通过保持编码器和解码器的浅层和程序的小体量来限制模型容量,而是使用损失函数来鼓励模型取得除了将输入复制到其输出之外的其他属性。在实践中,我们通常会使用稀疏自编码器。
简而言之,稀疏自编码器就是加入了正则项的自编码器,大部分参数置为0 ,这样做可以会使我们的自编码器学习数据的稀疏表示。
input_size = 784
hidden_size = 64
output_size = 784
x = Input(shape=(input_size,))
# Encoder
h = Dense(hidden_size, activation='relu', activity_regularizer=regularizers.l1(10e-5))(x)
# Decoder
r = Dense(output_size, activation='sigmoid')(h)
autoencoder = Model(input=x, output=r)
encoder = Model(input=x, output=h)在的隐藏层中,我们添加了一个l1激活值正则化矩阵(activity regularizer),它将在优化阶段对损失函数施加一个惩罚,与普通的自编码器相比,现在的表示方式更加稀疏。
3.3 卷积自编码器、变分自编码器(VAE)等
如果输入的是图像,使用卷积神经网络(CNN)作为编码器和解码器是很有意义的。在实际使用中,应用于图像的自动编码器始终是卷积自动编码器 ,因为它们的性能要好得多。
编码器将由Conv2D和MaxPooling2D层组成(最大池化用于下采样,以减小图像维度,降维),而解码器将由Conv2D和UpSampling2D(增加图像维度,升维)层组成。
而VAE是一类重要的生成模型(generative model),广泛地用于生成图像,而大名鼎鼎的GAN就是对抗生成模型。原理和实现都比较复杂,用于以后研究。
4. 总结
自编码器结构并不复杂,数学推导也很简单,有助于对于神经网络的理解。并且面对很多工业问题,比如说有大量的无标注数据,而有标签数据很少的情况下,可以利用自编码器进行预训练。

