三元组损失模型

• 论文素材提供：珍珍

三元组损失概述

三元组损失（Triplet loss）函数是当前应用较为广泛的一种损失函数，最早由Google研究团队在论文《FaceNet：A Unified Embedding for Face Recognition》所提出，常用在人脸识别任务中。目的是做到非同类极相似样本的区分，比如说兄弟二人的区分。

所以，Triplet loss的优势在于细节区分，即当两个输入相似时，Triplet loss能够更好地对细节进行建模，相当于加入了两个输入差异性差异的度量，学习到输入的更好表示，从而在上述两个任务中有出色的表现。

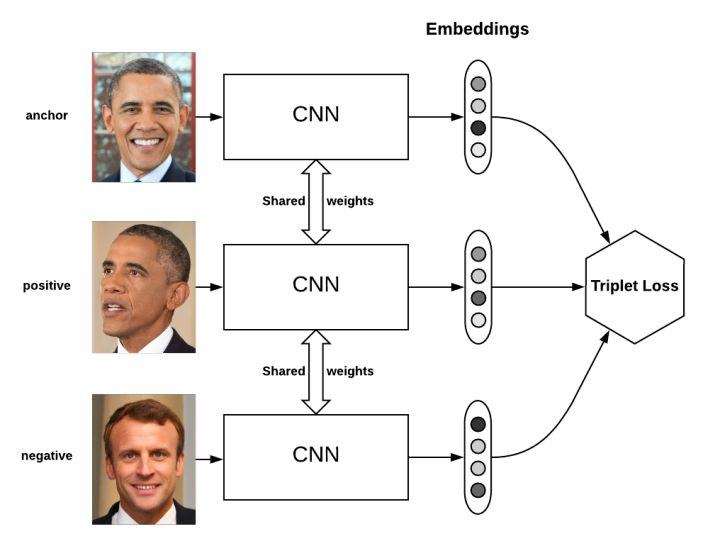
如上图所示，三元组图片输入到具有相同权重的特征提取网络。得到的特征向量再经过运算得到三元组损失（TripletLoss）。

基本思想

它的基本思想是：对于设定的三元组(Anchor, Positive, Negative) （Anchor和Positive为同类的不同样本，Anchor与Negative为异类样本），Triplet loss试图学习到一个特征空间，使得在该空间中相同类别的基准样本（Anchor）与 正样本（Positive）距离更近，不同类别的 Anchor 与负样本（Negative）距离更远。其思想与图像识别任务的目标很契合，即给定训练图集和测试图集，判断两张图片是否属于同一类标签。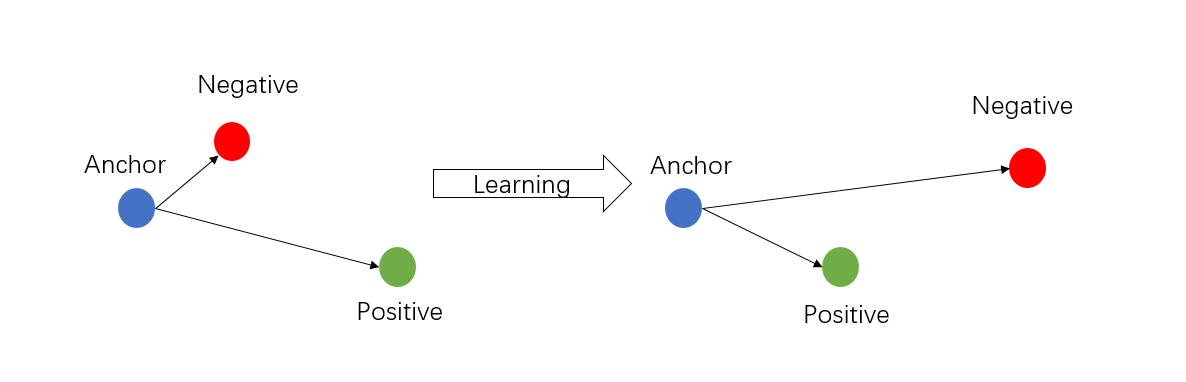

Triplet loss本质上是属于度量学习（Metric Learning）的范围，其借鉴了度量学习中的经典大间隔最近邻（Large Margin Nearest Neighbors，LMNN）算法。以Triplet loss为训练准则的深度神经网络模型既兼顾了度量学习的朴素性，又拥有神经网络优秀的非线性建模能力，能够在极大程度上简化并且控制模型训练过程。

优势

基于Triplet loss的神经网络模型可以很好的对细节进行区分，尤其是在图像分类任务中，当两个输入很相似的时候，Triplet loss对这两个差异性较小的输入向量可以学习到更好的表示，从而在分类任务中表现出色。

相比其他分类损失函数，Triplet loss通常能在训练中学习到更好的细微的特征feature，更特别的是Triplet loss能够根据模型训练的需要设定一定的阈值。
带Triplet loss的网络结构在进行训练的时候一般都会设置一个阈值margin，设计者可以通过改变margin的值来控制正负样本的距离。同时通过设定指定的阈值，可以在特征进行归一化后，用来判断是否为同一个标签。

缺点

虽然Triplet loss很有效，但也有缺点：三元组的选取导致数据的分布并不一定均匀，所以在模型训练过程表现很不稳定，而且收敛慢，需要根据结果不断调节参数，而且Triplet loss比分类损失更容易过拟合。

所以，大多数情况下，我们会把这种方法放在模型的预训练过程中，或者和softmax函数（分类损失）结合在一起使用。

理论推导

Triplet loss 由一个三元组构成，需要三张图片作为输入，如上一段中的图片所示，其中a: anchor 表示基准样本，p: positive 表示与anchor相同类别但不同的正样本，n: negative 表示与基准样本不同类别的负样本。利用生成的每个triplet，模型就能够创建出对应的positive pair 和negative pair 。

Triplet loss的目的是，在一定的距离（margin）上，将positive pair和negative pair分开,通过优化保证嵌入空间（Embedding Space）中类别相同的样本点之间距离足够近，而类别不同的样本点间距离足够远，即基准样本与负样本的距离要远远大于基准样本与正样本间的距离。

则Triplet loss的思想用欧氏距离形式化表示为：

$$L = max \lbrace d(a, p)-d(a, n) + margin\ ,\ 0 \ \rbrace$$

对于阈值margin的设置需要注意选择合适大小的值，理论上来说，较大的margin能够增强模型对不同类样本的区分度，但是如果在训练初期就将margin设置得比较大，则可能会增加模型训练的难度，进而出现网络不收敛的情况。在模型训练初期先使用一个较小的值对网络进行初始化训练，之后再根据测试的结果对margin的值进行适当的增大或缩小，这样可以在保证网络收敛的同时让模型也能拥有一个较好的性能。
在这里设样本为 $x$，$f(x)$为映射函数，整个训练集的大小为N，则每个triplet的输入，对应的Triplet loss形式化表示就可以写作：

$$\frac{1}{N} \{\quad \sum_i^N[|f(x_i^a) - f(x_i^p)|^2 - |f(x_i^a) - f(x_i^n)|^2 + \alpha]_+\quad\}$$

式中$|f(x_i^a) - f(x_i^p)|^2$表示的是2-范数的平方，其作用是计算欧几里得空间的长度或者向量的模，具体的展开形式为：$|\ast|^2 = |v_k|^2$
$v_k$表示的是向量，该式常用于机器学习的正则化中。
式中$ [\ast]+ $为合页损失（Hing loss）函数，表示与0取最大值，若式子小于 0,则说明此时的triplet满足损失值的要求，不同类别样本间的距离要远远大于相同类别样本间的距离，由于这样的triplet对神经网络的反向传播和参数更新没有提供帮助，因此将其损失值置为 0。至此我们可以看出，其实Triplet loss的整体优化目标就是一个最小化损失值的问题。

应用

在图像任务中，Triplet loss经常用作样本点在欧氏空间上的距离向量表示，它可以极大地提升深度特征的判别能力。为了使训练更加迅速有效，需要注意设计好训练策略，只选择合适的triplet进行训练，因为一个数据集的triplet组合非常多，全部进行训练的话会大大降低效率。

基于我们对Triplet loss的定义，一般而言，会将triplet分为三类，如图所示：

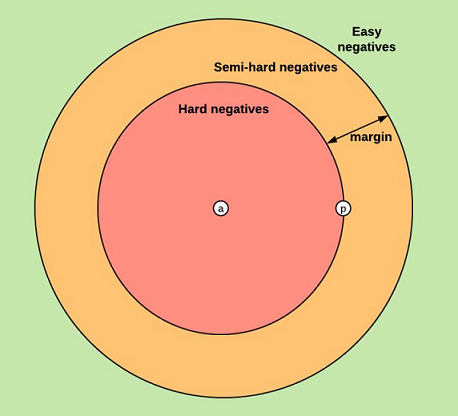
1、easy triplets （简单三元组）: 指在未经过训练的情况下，Triplet loss值已经为0的三元组，此时网络不需要训练学习就满足损失函数的要求。简单的用欧式距离表示为：$d(a, n)$>$d(a, p)$+ margin；

2、semi-hard triplets（一般三元组）: 指负样本与基准样本间的距离大于正样本与基准样本间的距离，但Triplet loss值还没有达到0，此时网络通过恰当的学习可以不断降低损失值。用欧式距离表示为：$d(a, p)$<$d(a, n)$ <$d(a, p)$+margin；

3、hard triplets（困难三元组）: 指负样本与基准样本间的距离小于正样本与基准样本间的距离，这是网络最难学习的样本组，此时的损失值会出现较大的震荡。用欧式距离表示为：$d(a, n)$ <$d(a, p)$。

由于简单三元组的损失值为0，如果训练网络只能学习到简单的triplets，会导致网络的泛化能力受到限制，网络没有学习到任何特征，对训练任务并没有帮助。因此当一个训练批次中包含大量的easy triplets时，会导致训练网络的收敛速度大大降低。

而一般三元组非常适合网络的前期训练，能够帮助训练网络的收敛，并且同时可以得到大量比较有效的统计信息。

困难三元组则在网络训练后期起到很好的学习作用，能够帮助提升网络的性能。让网络学习一些很难的样本特征，可以大大提高训练网络的分类能力，尤其是对难以判断的样本的判别能力。

因此，在网络的训练中，我们需要注意结合一般三元组和困难三元组，充分利用两者进行训练学习不仅能够加快网络的收敛，同时可以在很大程度上提升网络模型的识别性能。

但Triplet loss有一个缺点是，当数据集比较大时，训练的triplet数量也会随之变得十分庞大，此时会造成训练任务变得很艰难。而且如果采用随机选取三元组的训练策略，有可能很多次模型从训练集中挑选的三张图片，恰好是比较简单的三元组，计算出的损失值会很不稳定，从而导致模型很难学习到图片的主要特征。因此我们在使用Triplet loss函数时，要注意选取的训练集不宜过大，还要设计好训练策略来选择恰当的triplet。

三元组选取策略

许多类似的人脸识别、匹配工作都是在大数据集上实现的，这就要求对数据的高效利用。然而大多数样本在训练中后期不再有梯度贡献，例如含有margin的损失函数（triplet loss、softpn等），多数样本很容易满足于这个margin，此时损失函数中的loss不再发生变化，导致训练停滞阻塞。在极多identities（类别极多）的数据集中不能足够有效的挖掘困难样本，这就容易陷入局部极小，无法继续更新。

所以如何有效的进行困难样本挖掘（OHEM）成为了关键，困难样本应该包括同类（匹配样本）中距离较大的和非同类（非匹配样本）中距离较小的样本。

$$\frac{1}{N} \{\quad \sum_i^N[|f(x_i^a) - f(x_i^p)|^2 - |f(x_i^a) - f(x_i^n)|^2 + \alpha]_+\quad\}$$

对于上述的公式，实际上并没有体现困难挖掘，所以随机选取的样本并不能保证是困难样本，恰恰相反，这样选取的三元组实际上大部分为简单样本。

并且在大量图片样本下使用triplet loss也并非容易，如何有效的在large-scale情况下高效优化？使用triplet会发现数据量激增，可组合的三元组变多，如果要遍历所有组合是不现实的，或者极其低效 。

主要有两种方法，一是将triplet loss转为softmax loss（triplet net一文中，将triplet loss结合了softmax的输出与mse），另一种是batch OHNM。

直接考虑在所有的样本空间来sample一个batch，如果这个batch中有不满足margin的就认为是困难样本。然而这样做并不能保证采样时正好选取了很多很相似的样本，而且（a,p,n）图像组一经选取就已经固定，不会再有其他的组合，所以效率较低。所以寻找相似的个体（类别）是提高triplet net的核心关键。

对于含有10个个体（人）的人脸数据，难以区分的肯定是那些长的很像的个体（比如甲与乙为兄弟二人）。之前的困难挖掘是首先在这些打散的整体空间中随机设置（a,p,n）三元组然后成批去训练，分错的作为困难样本。这就使得你这些三元组都已经固定了，困难样本不一定是真的困难，除非运气好使得三元组中有很多甲、乙中的样本。所以一个想法是首先对于所有样本进行聚类，观察哪些样本比较接近，（甲和乙长得像肯定聚类结果很接近），那么我就在聚好类的子空间中选取(a,p)二元组组成batch，n在这个batch中来选取，那么这个负样本n就会是真正的困难样本。

How to Train Triplet Networks with 100K Identities?

上面这篇论文讨论了如何在大量类别上高效训练三元组网络。感兴趣的可以去看看。

1.随机选取

T代表全体样本空间，所以这里的三元组都是直接从总体样本中选择的，这也是我们大多数人的做法。

看上面这个图示，红色为anchor，浅绿色为positive，天蓝色为negative，深蓝色为hard negative。

这个方法中所有的匹配对和negative都是在整体样本中选取。可见，大多数negative是远离positive匹配对的，尽管训练的时候negative也会被分到一个batch中，但是真正困难的negative很难被选择到。

总结：在打散的整体样本空间随机选择三元组，并不是最好的选择方式，只是最方便而已。

2.Triplet with Batch OHNM

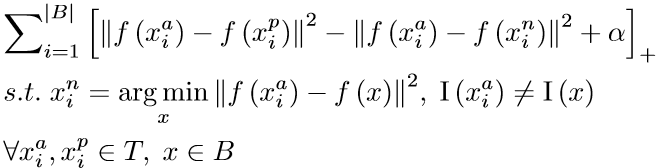
这个方法是为了在一个batch中尽可能挖掘困难样本，这时negative并非在整体样本中选取而是在一个batch中选择。

看上图公式的第三行，a和p$\in$T，表示从全体样本中选取，x$\in$B，表示x从batch中选取。

再看第二行，x与$x^a$属于不同类别，一个batch中，这样的x有数个，把每个x都与$x^a$计算相似度，取相似度最小的一个x为$x^n$，再用这个$x^n$与之前的$x^a$和$x^p$计算三元组损失。

就是说只在全体样本中选取一个batch的三元组，这些样本输入到网络，输出的特征进行比较，训练时在这一个batch的特征中再选择negative来训练。这实际上是有选择地选取negative样本。从全局搜索变成了局部有选择搜索，所以搜到的困难样本可能性更大。

举个例子：
设batch_size = 4，那么会有<$x_1^a$,$x_1^p$,$x_1$>, <$x_2^a$,$x_2^p$,$x_2$>, <$x_3^a$,$x_3^p$,$x_3$>, <$x_4^a$,$x_4^p$,$x_4$>共4个三元组，
然而，这些三元组并不是接下来用来计算三元组损失的三元组。

因为这12个样本均要先输入到网络中，得到他们编码后的特征，然后第一组的$x_1^a$与$x_1$、$x_2$、$x_3$、$x_3$分别计算相似度，其中最相似的一个作为第一组的$x_1^n$，其他组的negative通过同样的计算得到。

最终，可能用来计算损失的三元组变成了<$x_1^a$,$x_1^p$,$x_2$>, <$x_2^a$,$x_2^p$,$x_2$>, <$x_3^a$,$x_3^p$,$x_1$>, <$x_4^a$,$x_4^p$,$x_3$>，这样，我们就在一个batch内组合得到了最能实现困难样本挖掘的三元组。

首先是匹配对组成batch经过网络得到距离后，根据距离判断相似度，再重新组成三元组batch，输入到损失函数来优化。

有一点值得注意，某些情况下，直接选择与anchor最近的negative作为困难样本，可能会导致poor training，模型难以训练，应该选择比较近邻的样本。 通俗来说，就是特别相似的三张图反而无法训练，因为它们本来就模糊属于一个类，这样反而造成一种“错误标记”的训练样本，让模型原本训练得比较稳定的权重大幅度改变，反而不利于准确训练。

总结：在打散的整体样本空间随机选择二元组，在batch中选取合适的negative组成三元组，来计算三元组损失。