遍历算法
常规的遍历算法主要包括DFS和BFS。这两个算法不需要知道终结点在哪里,它会按照一定的模式挨个搜索,直到找到终结点。
举个不恰当的例子,遍历算法相当于你蒙着眼睛站在球场上,球场有一个球,需要你找到球,因为不知道球在哪,只能挨个找完所有位置。而启发式搜索需要一个启发函数,相当于睁开了眼睛,就可以直奔着球去了。
关于搜索算法的python实现已经放在了GitHub上:搜索求解算法
具体实现是用不同的搜索算法在网格地图上寻找终点。如A*算法的实现效果如下:
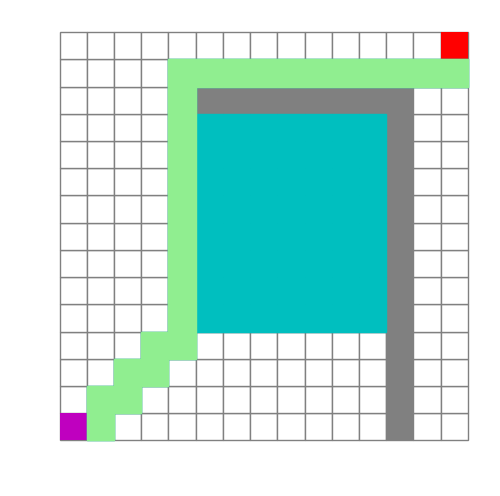
深度优先搜索(DFS)
深度优先,顾名思义即深度越大的节点会被优先扩展。在DFS中,使用栈(Stack)来实现上述特性。栈的特性是先进后出、后进先出。DFS过程中,会遍历当前节点的所有邻接节点,将它们依次压入栈中,遍历结束后,取出栈中最后一个元素,也就是最后一个被访问的邻接节点,继续递归。
DFS为数据结构中的基础内容,这里不再细说,遍历过程可以看下图(标号为第几轮遍历,橘黄色为寻找的路径):
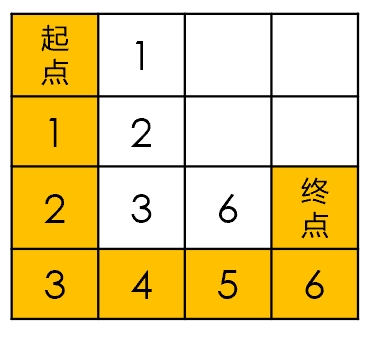
上图为DFS的遍历过程(按照左上右下遍历)与寻找到的路径。首先遍历起点的邻接节点,并标注为1(第一轮遍历),将下节点1(即栈尾)出栈,递归遍历,直到找到终点。
广度优先搜索(BFS)
广度优先会遍历完同级的所有节点,再增加深度。BFS中,使用队列(Queue)实现。队列的特性是先进先出、后进后出。BFS过程中,会遍历当前节点的所有邻接节点,将它们依次放入队列中,一轮遍历结束后,取出队列中第一个一个元素,也就是第一个被访问的邻接节点。
所以每一次的遍历,会遍历同一层所有节点的邻接节点。直到同一层的所有节点都已经遍历,才会遍历下一层的节点。看起来就像是一圈一圈地向外扩展。
BFS遍历过程如下图(标号为第几轮遍历,橘黄色为寻找到的路径):
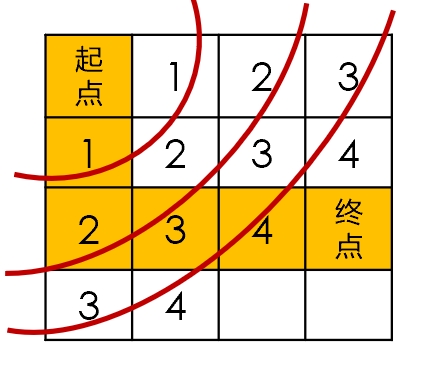
上图为BFS的遍历过程与寻找到的路径。首先遍历起点的邻接节点,并标注为1(第一轮遍历),将左节点1(即队首)出队列,遍历左节点1,其相邻的节点标注为2,排入队列中,直到找到终点。而在从终点向起点的回溯过程中(按照左上右下回溯),可以找到最短路径。
可以看出,一般而言,DFS遍历的节点较少,在某些节点没有遍历的情况下已经达到了终点。不过,找到的路径并非是最优路径。而BFS的遍历次数较多,但是回溯的时候可以找到最短路径。
DFS就像是一个孤军深入的莽夫,速度很快,一直向前冲,撞到南墙就回到上一步换个方向。BFS则稳扎稳打,步步为营,走得虽然很慢,但是可以找到最短路径。
Dijkstra算法
Dijkstra算法用来寻找图形中从一个顶点到其余各顶点的最短路径算法,一般用来解决两点之间(带权)最短路径问题。考虑这样一种场景,在一些情况下,图形中相邻节点之间的移动代价并不相等。
它既与BFS有相同之处,又与后面要介绍的贪婪最佳优先算法有一定相关性。
Dijkstra算法是这样运行的:把所有的点分成2类,一类称为S,指已经确定与起点之间最短路径的点集合,一类为U,指还没有确定与起点之间最短路径的点的集合。U中的点使用优先级队列表示,优先值为点到S的距离,如x到S的距离记作 $D{S-x}$ 。之后每次从U中取一个距离最小的点,比如n点,加入到S中<并更新n在U中的邻点x的值为$D{S-x} = \min(D{S-x}, D{x-n}+D_{S-n})$。依次迭代,直到U为空。
下面举个例子,如下为带权路径图(a为起点,i为终点):
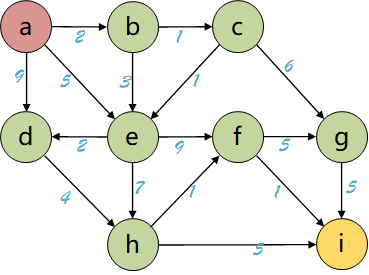
以上图为例,计算起点a到终点i的最短路径,箭头上的数值表示两个节点间的距离。
未与S中元素直接相连的点距离设置为正无穷。
第一轮选点,从优先队列U中选择值最小的b点放入S,并且更新b的邻点x的值为$\min(D{S-x}, D{x-b}+D_{S-b})$:
如邻点c,之前的$D{S-c} = \infty$,在b加入S之后的$D{S-c} = \min(\infty, 2+1) = 3$,故b点加入S集合之后的状态如下:
第二轮选点,从优先队列U中选择c点放入S,并且更新c的邻点x的值:
第三轮选点,从优先队列U中选择e点放入S,并且更新e的邻点x的值:
第四轮选点,从优先队列U中选择d点放入S,并且更新d的邻点的值:
第五轮选点,从优先队列U中选择g点放入S,并且更新g的邻点的值:
第六轮选点,从优先队列U中选择h点放入S,并且更新h的邻点的值:
第七轮选点,从优先队列U中选择f点放入S,并且更新f的邻点的值:
看上去,BFS与Dijkstra算法最显著的区别在于BFS使用了队列,而Dijkstra算法使用了优先级队列。实际上,使用不同的数据结构是为了各自取下一个点的方法而服务。
本质上,搜索算法和路径规划算法的目的都是如何正确地选取下一个节点。我们可以称评估如何选取下一个点的指标为代价函数$f(n)$,选取下一个点是要付出代价的,代价最小的点就是我们应该选取的点。
BFS算法之所以选择队列作为数据结构,是因为它每次选取的点为当前已经遍历的点的邻点,它的代价函数是当前点与起点的遍历轮数最小值。
Dijkstra算法之所以使用优先级队列,是因为它每次选取的点为从起点移动到当前点的最小值,也可以说是与已经遍历的点集合的距离最小的点。即它的代价函数是起点到当前点的移动代价。而当路径为无权时,移动代价就等于遍历轮数,即退化成了BFS。
启发式搜索
BFS和DFS的区别主要在于节点的弹出策略,根据弹出策略的区别,分别使用了队列和栈两种数据结构,而栈和队列作为两种相当基本的容器,只将节点进入容器的顺序作为弹出节点的依据,并未考虑终点位置等因素,这就使搜索过程与终点位置无关,变得漫无目的,导致效率低下。Dijkstra算法虽然可以解决带权的路径问题,却同样没有利用到终点位置信息,它的代价函数只与起点有关。而启发式搜索借助了一个启发函数,需要提前知道终点的位置,优化代价函数与起点和终点都有关,这样可以更快达到终点。
贪婪最佳优先算法
贪婪最佳优先算法(Greedy Best First Search, GBFS)的特点是评价函数=启发函数。
设评价函数为$f(n)$,启发函数为$h(n)$,那么令$f(n)=h(n)$。即从当前节点出发,寻找下一个邻接节点,邻接节点选择的依据(评价函数)为使得启发函数值最最小的节点。
之所以贪婪最佳优先算法的速度一般会比较快,是因为启发函数使用了当前点与终点的信息。
同样以寻找路径为例:
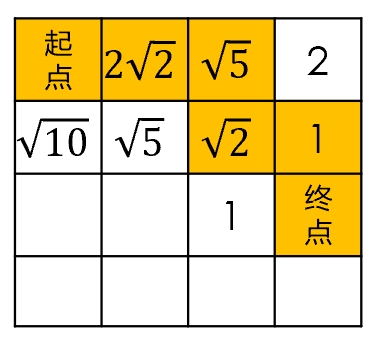
上图为使用贪婪最佳优先算法寻找的路径(橙色标注),有数值的格子表示被遍历到的节点,数值表示该点与终点的欧氏距离,即启发函数$h(n)=$欧氏距离。
首先在起点处,计算邻点的$h(n)$,由于起点右侧的点距离小于其他邻点,即$h(n)$最小,又由于$f(n)=h(n)$,故该点的代价函数最小,因此选择该点作为下一个点。然后重复上述过程,直到达到终点。
可以看到,由于设置代价函数=启发函数,使得寻找过程中被遍历的点减少了,也就是说,这个算法可以直奔终点快速前进。
当然,这个算法也有不足之处:1.寻找的路径常常不是最优解,2.启发函数最小化这一目标对于错误的起点比较敏感,不同的起点对于路径寻找过程影响很大,甚至有可能进入死循环,3.最坏情况下复杂度很高为$O(b^m)$,b为节点分支因子数、m为搜索空间的最大深度。
实际的地图中,常常会有很多障碍物,因为代价函数只与启发函数有关,而启发函数只表示当前位置与终点的关系,所以GBFS就很容易陷入局部最优的陷阱。下图的地图中有一个专门设置的局部最优陷阱,很显然GBFS虽然搜索速度够快,但是找不到最优路径。

针对这些不足之处,最重要的是需要设计一个良好的启发函数。
A*算法
英语不错的同学可以直接看一看这篇:Introduction to the A* Algorithm
GBFS用节点到目标点的距离作为代价函数,将搜索方向引向目标点,搜索效率高;而Dijkstra算法采用起点到当前扩展节点的移动代价作为代价函数,能够确保路径最优。
那么可不可以将两者的代价函数进行融合,从而在保证路径最优的同时提高搜索效率?答案是肯定的,融合后的算法就是A*算法。
A*算法的代价函数为$f(n) = g(n) + h(n)$,g(n)为起点到当前节点的移动代价,$h(n)$为启发函数,表示从当前点到终点的距离函数。
其中,若将$g(n)$置为0,则A*算法退化成贪婪最佳优先算法,若$h(n)=0$,则退化成Dijkstra算法。
能否找到最优路径的关键是启发函数$h(n)$的选取,如果$h(n)$始终小于等于节点n到终点的代价,则A*算法保证一定能够找到最短路径。但是当$h(n)$的值选取不合适,会导致算法将遍历越多的节点,也就导致算法越慢。
由于A* 算法的启发函数是位置上的距离,因此在不带位置信息的图数据中不适用。
A*算法描述如下:
* 初始化open_set和close_set;
* 将起点加入open_set中,并设置优先级f(n)为0(优先级最高);
* 如果open_set不为空,则从open_set中选取优先级最高的节点n:
* 如果节点n为终点,则:
* 从终点开始逐步追踪parent节点,一直达到起点;
* 返回找到的结果路径,算法结束;
* 如果节点n不是终点,则:
* 将节点n从open_set中删除,并加入close_set中;
* 遍历节点n所有的邻近节点:
* 如果邻近节点m在open_set中,则:
* 比较g(n)是否比原来更小,如果更小则更新其g(n)、优先级f(n)和其父节点
* 如果邻近节点m在close_set中,则:
* 跳过,选取下一个邻近节点
* 如果邻近节点m不在open_set和close_set中,则:
* 设置节点m的parent为节点n
* 计算移动代价g(n)
* 计算节点m的优先级f(n)
* 将节点m加入open_set中对于网格形式的图,有以下这些启发函数可以使用:
- 如果图形中只允许朝上下左右四个方向移动,则可以使用曼哈顿距离(Manhattan distance)。
如果图形中允许朝八个方向移动,则可以使用对角距离。
如果图形中允许朝任何方向移动,则可以使用欧几里得距离(Euclidean distance)。
最优遍历点:
对于下图:
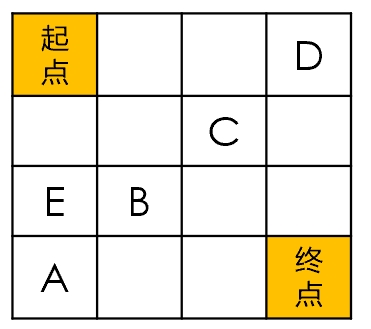
假设路径函数$g(n)$和启发函数$h(n)$都使用曼哈顿距离,且$f(n)=g(n)+h(n)$。
首先,对于B点和E点,当它们都在open_set时,应该选取哪一个点作为下一个路径点呢?E与B的代价函数f(n)相等,而直觉上应该选择B点,因为第一行第三列与E点是等价的,选择E点必然也可以选择它,而这样会大大增加遍历次数。B点的启发函数小于E,而路径函数大于E,为了使得B点可以优于E点,我们需要使得B点减少的启发函数代价要多于其增加的路径代价。
其次,对于A、B、C、D四点来说,$f(A)=f(B)=f(C)=f(D)$,并且四点的启发函数也相同,那么在这种情况下,当四个点都在open_set中时,又该如何选取呢?如果我们更倾向于选择B、C,那么需要使得它们的代价更小。
针对上述2点,我们可以改变路径函数,比如使用对角距离作为路径函数,则E、B/C、A/D的代价函数2+4、2.4+3、3+3(路径+启发函数),即可实现选取B/C作为更优点的目的。
或者,在不改变路径函数的情况下,在代价函数相同时,使用额外的约束条件。比如路径和启发函数都为曼哈顿距离,则E、B/C、A/D的代价函数相同,此时取其中到终点对角距离最小的点最为最优点即可选出B/C。
最短路径:
关于A*算法能否找到最短路径最重要的一点就是已经处于open_set的邻点的更新。也就是如果遍历到的邻点在open_set中,要比较现有路径和原路径哪一个更短,取更短的路径的上一个节点作为父节点。
以下举个例子:假设在A点处遍历到邻点B,且B没有加入openset,则的B父节点设置为A。一段时间后,在C点处也遍历到了B,则比较$g(c)+D{C-B}$和$g(A)+D{A-B}$,若$g(c)+D{C-B}$更小,则应该更新B的父节点为A。
关于GBFS和A*算法在路径寻找过程中的差别可以参看下图:
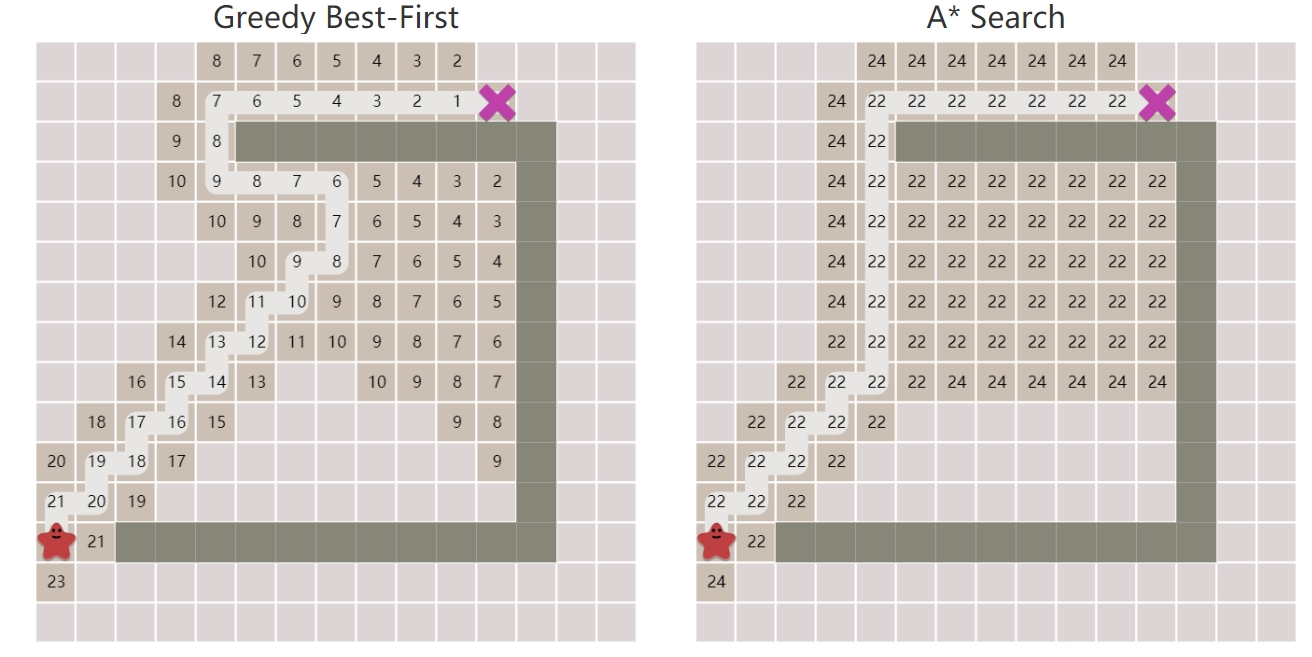
上图为GFBS和A*算法正有障碍路径寻找过程中,每个节点的代价函数。可以看到,使用GBFS之后,路径上的节点的代价函数随着接近终点会逐渐减小,但是却无法找到最优路径。
